倚在地铁车窗上,一个半小时的地铁通勤终于到了最后一站。在临近下车的前面几站是高架地铁,车厢从黑乎乎的隧道里驶出来,车窗外的夜色也开始涌入。
从窗户向外看,路灯和马路旁暗淡的灌木飞速朝后移动,又经过了花梨坎站附近,看到远处那个名叫“金*公务”的地方,红色的标题赫然立在墨色的远方,因为太远了,第二个字始终看不清楚,从上个冬天到这个夏末,我反复猜测,是“金鹰”吧?不对,看着又有点像“金顺”,毕竟这里是顺义区……不知道猜测了多少次,其实挺希望有个机会靠近这个地方,确认下那个字是啥。
不同于往常的是,今天心情不错,发现了一个新现象。路灯黄色的光在快速向后流动,但是车窗右上角那个半圆形的图案为何保持不动呢?我定睛一看,那是今天的月亮。
为什么月亮没有跟其他物体一样也向后流动呢?以前确实听过“月亮走,我也走,我给月亮赶牲口,一赶赶到马山口”的童谣,但是没想到月亮能走得这么快,跟飞速的地铁保持同频共进,跟我的相对速度为零。这是为什么呢?
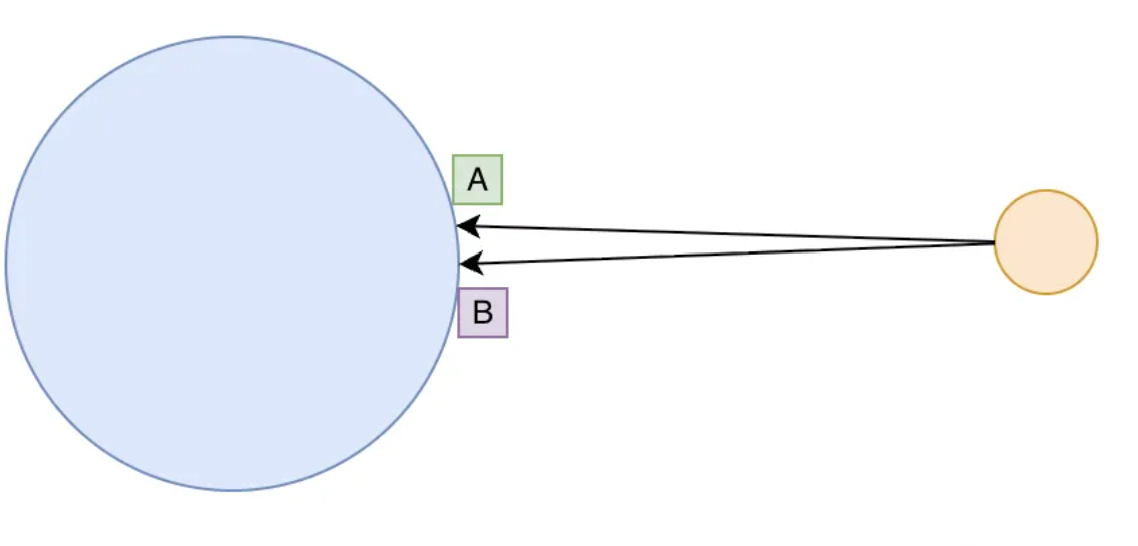
回来思考(+检索)了下,月亮之所以看着不动,是因为距离地球太远了,这里的“远”是一个相对概念,比较的对象是我在地球表面移动的单位距离。换言之,就是在我观察月亮的那段时间内移动的总距离(上图A和B两点之间在地球表面的距离),这段距离相较于地球和月亮之间的距离太短以至于可以忽略不计,因为AB弧线长度=地月距离d*θ => 分母d太大,这就导致A-Moon-B这个角度θ太小。人眼需要通过双眼的视差才能感知运动(视差是指从两个不同位置观看同一物体的方向之差,这里就是A和B两位置),月亮太远,导致方向差θ太小,时差接近0,所以视觉上感觉不到月亮移动。
那自然而然就有另一个疑问了:当我的运动速度到了什么水平,才能“摆脱”尾随的月亮?根据上面的思考过程,那就是θ这个角度能够大于人眼感知的差异阈值,但这个角度阈值对应的速度是多少呢?
去问了下DeepSeek,它的回答涉及了人眼角分辨率以及角位移的概念。
**人眼角分辨率 (δ)**:这是人眼能分辨的两个点之间的最小角度差。对于视力极佳(如1.0或20/20视力)的人来说,这个阈值大约在 0.016° 到 0.02° (约 0.00028 到 0.00035 弧度)之间。小于这个角度,两个点(或同一个点在两个位置)就会被人眼融合,感觉是静止不动的。
角位移 (θ):当从A点移动到B点,观察者与月亮的连线所扫过的角度就是角位移 θ。其计算公式为:θ ≈ AB / d (当θ很小时,弧度制下近似成立)。由于地月距离 d ≈ 384,400 km 这个分母极其巨大,即使您移动了很长一段距离(比如AB=100 km),θ角依然会非常小(约0.00026弧度或0.015度)。
要让月亮看起来“摆脱”观察者的运动,不再尾随,就需要移动产生的角位移 θ 大于人眼的角分辨率 δ。即: θ > δ
- 地月距离 d = 384,400,000 米
- 人眼角分辨率 δ = 0.02°(我们取一个较为保守的估计值,确保大多数人能感知)
- 首先将 δ 转换为弧度:δ = 0.02 × (π / 180) ≈ 0.000349 弧度
1)计算所需的最小位移 (Δx)
根据公式 θ = Δx / d
令 θ = δ
则 Δx = δ × d = 0.000349 × 384,400,000 ≈ 134, 155 米
这意味着,需要垂直于观察者与月亮连线的方向移动大约 134公里(即AB弧线长度),才能让月亮在天幕上的位置产生一个刚好能被察觉的变化。
2) 计算所需的速度 (v)
关键点在于:这个位移必须在远小于人视觉暂留和运动感知时间尺度内完成。如果希望这个变化是“实时”的、能被感知为“运动”而非“跳跃”,那么这个位移时间应该短于几秒钟。假设希望在 1秒 内完成这个最小可察位移,从而清晰地看到月亮“动了一下”:
- 所需速度 v = Δx / t = 134,155 米 / 1秒 ≈ 134 km/s
- 这个速度是音速的约390倍。
- 是第一宇宙速度(7.9 km/s)的约17倍。
- 是第二宇宙速度(11.2 km/s)的约12倍。
即使把时间放宽到10秒,所需速度仍然高达 13.4 km/s,这依然远超任何常规交通工具的极限,达到了航天器的级别。
好吧,结论出来了,看来我需要达到13.4km/s的速度才能在地面上感知到月亮的运动,看起来不离开地面是做到了,貌似坐飞机也不行呐hhh
怪不得“月亮走,我也走”呢!